Per vedere come si propagano gli errori nelle somme e nelle
differenze consideriamo il seguente esempio.
Supponiamo di avere le misure dirette (x e y) delle
due grandezze di cui si vuol calcolare la somma così espresse:
x=
y=
Se chiamiamo z la grandezza pari alla somma di x
e y, abbiamo che il valore "più alto" probabile
per z si ha quando x e y assumono i loro
valori più grandi, cioè per 
+
e 
+
valore massimo probabile=(+++)=(+)+(+)
mentre il valore "più basso" probabile si ha quando
entrambe x e y assumono il loro minino ossia - e -,
percui si ha
valore minimo probabile=(-+-)=(+)-(+)
osservando i due valori (massimo e minimo) ricavati si vede
che per la grandezza derivata z=x+y=
abbiamo
=+
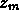e
+
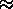
Si può operare in modo analogo per calcolare l'errore commesso nel caso di una differenza e si raggiunge lo stesso risultato. Possimo allora definire la regola della composizione degli errori in una somma o in una differenza, generalizzando il risultato ottenuto a somme o differenze di N termini, nel modo seguente:
, , ... , 
e tali valori vengono utilizzati per calcolare quantità
del tipo +...++
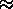
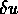+...+Si è usato il simbolo di uguaglianza approssimata (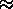) per
sottolineare il fatto che quella che è stata fornita è una
valutazione un po' "grezza" dell'errore : vedremo più
avanti che esiste una stima migliore costituita dalla somma
quadratica (o somma in quadratura) dei singoli errori.
Per ora accontentiamoci della definizione data con la
consapevolezza che essa rappresenta un limite superiore
per la valutazione dell'errore valido in qualsiasi caso.
Propagazione degli errori
Errori
nei prodotti e quozienti