LA LEGGE DI POISEUILLE

Il moto a velocità costante di un fluido viscoso ed
incomprimibile in una tubatura di sezione costante è
laminare: consiste cioè nello scivolamento relativo
di un numero infinito di cilindri coassiali all'asse del tubo.
La variazione 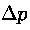 di pressione tra due punti situati
rispettivamente all'ingresso ed all'uscita del tubo è data da:
di pressione tra due punti situati
rispettivamente all'ingresso ed all'uscita del tubo è data da:
![delta p=[(8*eta*L)/(pi*r*r*r*r)]* Q(v)](/mflu/imgs/formule/poise.gif)
detta legge di Poiseuille,
dove L è la lunghezza del tubo, r il suo raggio,
 il coefficiente di viscosità del fluido e
Qv la portata del tubo.
il coefficiente di viscosità del fluido e
Qv la portata del tubo.
È possibile convincersi della ragionevolezza di questa relazione
attraverso un'analisi dimensionale.
Riscrivendola come:
![Q(v)=[(pi*r*r*r*r)/(8*eta)]*(delta p/L)](/mflu/imgs/formule/poiseinv.gif)
si può verificare che le grandezze devono comparire
nella formula con le potenze indicate ipotizzando ragionevolmente che
la portata del condotto (volume di fluido che attraversa la sezione
nell'unità di tempo) sia direttamente proporzionale ad una qualche
potenza da determinarsi della propria viscosità, del raggio della
tubatura e del gradiente di pressione (variazione di pressione in rapporto
alla lunghezza del tubo):
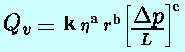
secondo una costante di proporzionalità k da determinarsi
sperimentalmente. Riducendo le quantità elencate alle dimensioni
fondamentali si ha:
L³ T-1= (M L-1 T-1)a
Lb (M L-2 T-2)c
Imponendo la coerenza dimensionale dei fattori corrispondenti nei due
membri si ottiene:
| per L | 3 = - a + b -2c
|
| per T | -1 = -a - 2c
|
| per M | 0 = a + c
|
sistema che risolto dà a = -1, b = 4 e c = 1,
proprio come nell'equazione sopra, posto il coefficiente
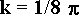 .
.
Ricordando che si era detto:
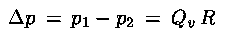
dall'equazione di Poiseuille possiamo definire il fattore
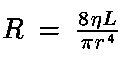
detto resistenza idraulica. La legge di Poiseuille può
essere interpretata come legge di proporzionalità tra la "causa"
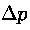 che provoca il flusso e l'effetto
Qv che ne segue secondo una costante di
proporzionalità R che dipende dalle caratteristiche
geometriche del condotto e dalla viscosità del fluido.
Si noti che la legge di Poiseuille è analoga alla legge di Ohm
per la conduzione elettrica, alla legge di Fick per la diffusione di
un soluto e al postulato di Fourier per la conduzione del calore.
che provoca il flusso e l'effetto
Qv che ne segue secondo una costante di
proporzionalità R che dipende dalle caratteristiche
geometriche del condotto e dalla viscosità del fluido.
Si noti che la legge di Poiseuille è analoga alla legge di Ohm
per la conduzione elettrica, alla legge di Fick per la diffusione di
un soluto e al postulato di Fourier per la conduzione del calore.
 Esercizi
Esercizi
 Esempi
Esempi
 Storia
Storia
 Fluidi viscosi > Il moto vorticoso
Fluidi viscosi > Il moto vorticoso
 Fluidi viscosi < Il coefficiente
di viscosità
Fluidi viscosi < Il coefficiente
di viscosità
 Indice
Indice
Copyright © I.S.H.T.A.R. - March, 1999
 di pressione tra due punti situati
rispettivamente all'ingresso ed all'uscita del tubo è data da:
di pressione tra due punti situati
rispettivamente all'ingresso ed all'uscita del tubo è data da:
![delta p=[(8*eta*L)/(pi*r*r*r*r)]* Q(v)](/mflu/imgs/formule/poise.gif)
 il coefficiente di viscosità del fluido e
Qv la portata del tubo.
il coefficiente di viscosità del fluido e
Qv la portata del tubo.![Q(v)=[(pi*r*r*r*r)/(8*eta)]*(delta p/L)](/mflu/imgs/formule/poiseinv.gif)
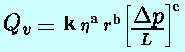
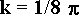 .
.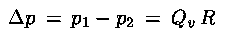
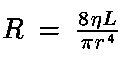
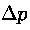 che provoca il flusso e l'effetto
Qv che ne segue secondo una costante di
proporzionalità R che dipende dalle caratteristiche
geometriche del condotto e dalla viscosità del fluido.
Si noti che la legge di Poiseuille è analoga alla legge di Ohm
per la conduzione elettrica, alla legge di Fick per la diffusione di
un soluto e al postulato di Fourier per la conduzione del calore.
che provoca il flusso e l'effetto
Qv che ne segue secondo una costante di
proporzionalità R che dipende dalle caratteristiche
geometriche del condotto e dalla viscosità del fluido.
Si noti che la legge di Poiseuille è analoga alla legge di Ohm
per la conduzione elettrica, alla legge di Fick per la diffusione di
un soluto e al postulato di Fourier per la conduzione del calore. Esercizi
Esercizi
 Esempi
Esempi
 Storia
Storia