Variabili aleatorie continue di cui è noto a priori che i loro valori possibili appartengono ad un dato intervallo e all'interno di questo intervallo tutti i valori sono equiprobabili, si dicono distribuite uniformemente o che seguono la distribuzione uniforme.
Consideriamo una variabile aleatoria X soggetta ad una
legge di distribuzione uniforme nell'intervallo (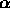
,
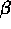) e scriviamo l'espressione dela densità di probabilità p(x).
Questa funzione dovrà essere costante ed uguale, diciamo, a c
nell'intervallo (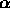,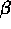) e nulla al di fuori di
esso, percui
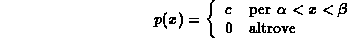
Poichè per la condizione di normalizzazione, l'area delimitata dalla curva di distribuzione deve essere uguale all'unità si ha
da cui risulta
La densità di probabilità p(x) assume quindi la forma
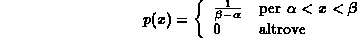
Caratteristiche della
distribuzione
Esempi
Determiniamo le caratteristiche numeriche fondamentali della
variabile aleatoria X soggetta alla legge di distribuzione
uniforme nell'intervallo (,).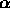
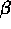Il valor medio, applicando la definizione di momento iniziale di ordine 1 nel caso di variabili continue, vale
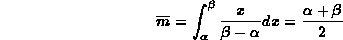
In virtù della simmetria della distribuzione il valore della mediana coincide con quello del valor medio. Si tenga inoltre presente che la distribuzione uniforme non ha moda.
ora, attraverso il momento centrale di ordine 2 nel caso continuo, calcoliamo la varianza e da questa la deviazione standard:
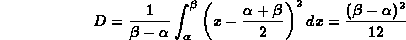
da cui la deviazione standard
). 
|
Principali
distribuzioni continue
