|
Leggi di Kirchhoff
|
|
|
Consideriamo un sistema composto da più conduttori percorsi da corrente e da una o più sorgenti di f.e.m. (generatori); tale sistema prende il
nome di rete ed ogni conduttore prende il nome di ramo della rete, costituito da una disposizione in serie di elementi attivi (generatori) e
passivi (resistenze), o, eventualmente, di un solo tipo di elemento.
|
|
|
I rami si incontrano in punti detti nodi o diramazioni. Un nodo è composto da almeno tre rami.
Una maglia è l’insieme di
più rami della rete che formano un circuito chiuso non ulteriormente divisibile in parti chiuse.
|
|

|
|
|
Prima legge di Kirchhoff (legge dei nodi):
|
|
|
|
La somma algebrica delle intensità di corrente nei rami facenti capo allo stesso nodo è nulla.
|
|
|
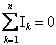
|
|
|
|
Siano I1, I2, I3, … In le intensità di corrente degli n rami di un nodo. Queste sono considerate positive
se entranti nel nodo, negative se uscenti.
Per spiegare il concetto di somma algebrica, osserviamo il seguente esempio:
|
|
|
|
|
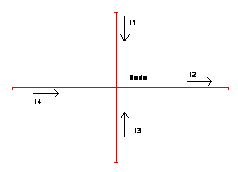
Le correnti entranti sono I1, I3 ed I4. Nella sommatoria sono addizionate.
La corrente uscente è I2 . Nella sommatoria è sottratta.
La prima legge di Kirchhoff è così tradotta:
|
|
|
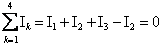
|
|
|
|
La legge dei nodi è una diretta conseguenza della legge di conservazione della carica; infatti la quantità di carica che entra in un nodo è uguale alla quantità di carica che ne esce; in altre parole nel nodo non c’è accumulo né diminuzione di carica. Per questo motivo, in un dato intervallo di tempo Δt, la corrente entrante in un nodo deve essere uguale a quella uscente.
|
|
|
|
Seconda legge di Kirchhoff (legge delle maglie):
|
|
|
|
La somma algebrica delle f.e.m. agenti lungo i rami di una maglia è uguale alla somma algebrica dei prodotti delle intensità di corrente di ramo
per le rispettive resistenze (del ramo).
|
|
|
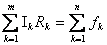
|
|
|
|
In altre parole:
|
|
|
|
In ogni maglia la somma algebrica degli incrementi di potenziale è uguale alla somma delle diminuzioni di potenziale.
|
|
|
|
Se prendiamo un punto arbitrario X di una maglia, sia Vx il potenziale in X e immaginiamo di percorrere tutta la maglia in un senso o
nell’altro e di ritornare in X, il potenziale sarà ancora Vx.
|
|
|
|
Se nel percorrere le maglie si sono incontrate n f.e.m. la cui somma algebrica
è 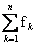 , si dovranno incontrare anche m cadute
di tensione , si dovranno incontrare anche m cadute
di tensione
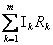 , tali che la differenza con le f.e.m. si annulli. , tali che la differenza con le f.e.m. si annulli.
|
|
|
|
Per spiegare la II legge di Kirchhoff, si focalizza l’attenzione su una maglia della rete e si fissa ad arbitrio una corrente di maglia con un verso di
scorrimento positivo. Per ogni ramo della maglia valgono le seguenti definizioni:
- La corrente di ramo è positiva se concorde con il verso della corrente di maglia, altrimenti è
negativa.
- Le forze elettro-motrici di ramo sono positive se la corrente di maglia attraversa i generatori dal polo negativo al
polo positivo, altrimenti sono negative.
|
|
|
|
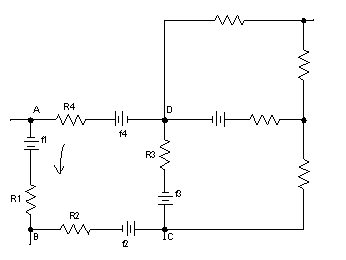
Esempio:
|
|
|
|
|
|
Si consideri la maglia ABCD e si fissi un verso arbitrario positivo di corrente di maglia (per esempio il verso antiorario).
La II legge di Kirchhoff è:
|
|
|
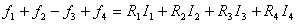
|
|
|
|
È un'equazione che si può ottenere anche mettendo a sistema la legge di Ohm per i quattro rami della maglia:
|
|
|
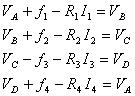
|
|
|
Osservazioni:
|
|
Quante maglie ha una rete?
Detto N il numero di nodi ed R il numero di rami della rete, il numero di maglie è M=R-(N-1)
|
|
Come individuare il numero di maglie indipendenti?
Partendo da una maglia, si individuano successivamente le altre in modo che ciascuna nuova maglia possegga almeno un ramo della rete che non fa parte
delle precedenti.
Se N è il numero dei nodi, solo N-1 sono indispensabili per scrivere equazioni indipendenti per le correnti.
|
![]()