

La distribuzione ipergeometrica si applica ad insiemi
contenenti N elementi divisi in due classi: in una abbiamo
M oggetti che presentano una certa caratteristica e
nell'altra si trovano gli altri N-M elementi con
caratteristiche diverse da quella che contraddistingue gli
oggetti della prima classe.
Se ci si chiede quale sia la probabilità di trovare x
elementi appartenenti alla prima classe, effettuando
un'estrazione, senza reintroduzione, di campione a caso di n
elementi dagli N totali, bisogna utilizzare alla
distribuzione ipergeometrica.
La forma matematica di tale distribuzione è la seguente:

Si noti bene che a differenza del caso della distribuzione binomiale, ciascuna delle n estrazioni non sono indipendenti l'una dalle altre.
Ricordiamo che con la scrittura 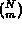 indichiamo il coefficiente
binomiale
indichiamo il coefficiente
binomiale 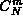

Una proprietà dei coefficienti binomiali che ci sarà utile per i calcoli successivi è la seguente:
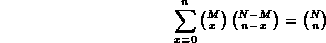
Calcoliamo il valor medio della distribuzione utilizzando la definizione del momento iniziale di ordine 1:
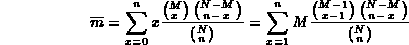
ponendo y = x - 1 otteniamo
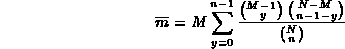
Dalla proprietà dei coefficienti binomiali, otteniamo
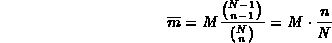
Per quanto riguarda la deviazione standard, dopo lunghi e tediosi calcoli si arriva a
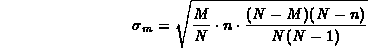
Soluzione. Applicando la formula della distribuzione ipergeometrica con i dati forniti nel testo otteniamo
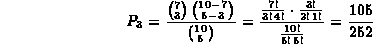
Cioè la probabilità di estrarre un campione di 5 palline contenente 3 palline bianche è pari a 105/252 (=2/5) ossia poco meno del 42%.
Soluzione . Per calcolare la probabilità che
almeno 2 palline del campione siano bianche, utilizziamo
il teorema della somma
delle probabilità considerando un campione con almeno
due palline bianche.
In particolare i casi possibili sono: 2 palline bianche
su 5, 3 su 5, 4 su 5 oppure tutte e 5 bianche. allora la
probabilità richiesta saraà
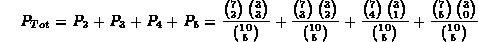
Eseguendo i calcoli otteniamo
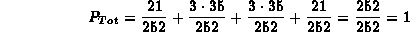
Questo risutato non deve stupirci in quanto, essendo solo 3 le palline nere contenute nell'urna, al momento dell'estrazione di 5 palline per forza almeno 2 palline dovranno essere bianche!!!
Se infatti ci chiedessimo quale sia la probabilità di estrarre un campione di 5 palline contenente solo una pallina bianca, ci troveremmo di fronte al fattoriale di un numero negativo che sappiamo essere privo di significato (l'esercizio è lasciato allo studente).