

Il coefficiente binomiale che compare nell'omonima distribuzione deriva dall'espansione del binomio di Newton (p+q)N in N+1 termini: tale sviluppo si può scrivere come
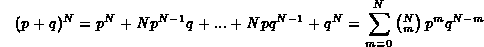
e vale per due numeri qualunque p e q e ogni intero positivo n.
La distribuzione binomiale dà la probabilità di ottenere m successi in n prove, quando p è la probabilità di successo in una singola. Il valor medio di tale distribuzione, corrispondente al numero medio di successi, si ricava attraverso il momento iniziale di ordine 1:
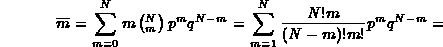
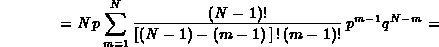
Ponendo m - 1 = r otteniamo
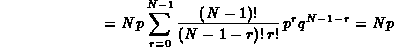
Infatti l'ultima sommatoria è equivalente all'espansione del binomio di Newton
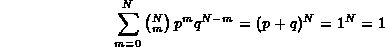
considerato nel nostro caso in cui la somma p+q è uguale ad
uno.
Così come abbiamo ricavato il valor medio di successi in N
prove, attraverso il momento
centrale di ordine 2 si può ricavare
la deviazione standard.
Si ottiene così come valore della deviazione standard:

In generale la distribuzione binomiale non è simmetrica
salvo il caso in cui, tipico ad esempio del lancio della moneta,
p sia uguale ad 1/2.
Soluzione. In questo caso bisogna prestare attenzione ad un particolare: in questo esempio ci viene richiesta la probabilità che almeno due stazioni siano funzionanti. Per fare questo applichiamo il teorema della somma alle probabilità dei seguenti eventi:
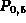 )
) 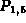 )
) 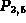 )
) 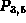 )
) La somma delle probabilità di questi quattro eventi ci dà la probabilità che cerchiamo (P) ossia che almeno due stazioni siano funzionanti.
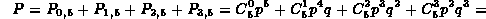
Cioè la probabilità che almeno due stazioni mantengano la comunicazione ad un dato istante è circa il 26%.

Mostrare che la distribuzione degli articoli fallati riportata nella tabella è assimilabile ad una distribuzione di tipo binomiale e determinare la percentuale di articoli prodotti dalla macchina e affetti da qualche difetto.
Soluzione. Dalla tabella riportata calcoliamo quanti articoli difettosi sono stati raccolti in 100 campioni e, di seguito, dividendo per il numero totale dei campioni prelevati, la media della distribuzione empirica riportata in tabella:
(0+32+14+6+4+0) /100 = 0.56
Se ora supponiamo che tale distribuzione sia modellizzabile attraverso una distribuzione binomiale, il valore medio di articoli difettosi per ogni campione che ci aspetterebbe è Np: qui N è uguale al numero di articoli per ogni campione cioè 5, percui il calcolo di p (probabilità di trovare un articolo difettoso in un campione di cinque oggetti) è immediato e si ricava:
Ovviamente in questo caso q=8/9 e con questi valori di p e q andiamo a calcolare lo sviluppo del binomio di Newton (p+q)Nche ci da la distribuzione binomiale che noi abbiamo ipotizzato:
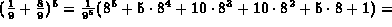
in questo modo, la nostra distribuzione ipotetica ci dovrebbe dare, su 100 campioni di cinque oggetti ciascuno, 55 campioni privi di articoli difettosi, 35 con un articolo difettoso, 9 con due articoli difettosi, 1 con tre oggetti fallati e nessun campione con quattro o cinque articoli difettosi.
I dati così ottenuti si conformano alla distribuzione sperimentale trovata dagli addetti ai controlli: possiamo quindi riassumere dicendo che la distribuzione è approssimativamente binomiale e la percentuale di articoli difettosi prodotti dalla macchina è stimabile con il valore di p che abbiamo ottenuto, cioè circa 11%.