DISTRIBUZIONI DISCRETE
- Distribuzione di Poisson -

La distribuzione Poisson è in accordo terzo assioma della probabilità. Facendo la sommatoria su tutti gli eventi possibili otteniamo:

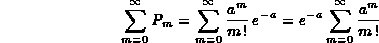
Ma la serie in m è proprio la serie che definisce e^a percui

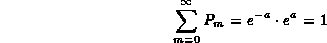
Vediamo qual'è il valor medio della distribuzione di Poisson avvalendoci del momento iniziale di ordine 1:

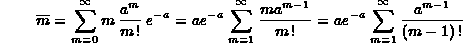
Si noti che ora la sommatoria parte da 1 in quanto il termine corrispondente a m=0 è nullo. Se poniamo m-1=k l'ultima serie è di nuovo la sommatoria che definisce e^a, percui:

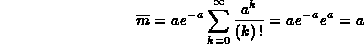
Ricorrendo alla definizione del momento centrale di ordine 2, si può dimostrare che la deviazione standard è uguale alla radice quadrata del parametro caratteristico della distribizione di Poisson

• Esempio 1. Supponiamo di voler calcolare la probabilità che una qualsiasi persona adulta abbia bisogno del medico nell'arco di un anno. Utilizziamo a questo scopo alcuni dati rilevati a Philadelphia nel 1967 e riportati nella tabella seguente:
  Visite mediche, Philadelphia 1967
  

  Queste cifre si adattano alla distribuzione di Poisson: il numero di persone che va dal medico è positivo e inoltre è piccolo rispetto al totale del campione (il massimo della distribuzione è proprio sullo 0!).

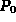  Dalla tabella risulta che =a=116/100=1.16: ne segue che la probabilità che una persona a caso non abbia mai bisogno del medico nel corso di un anno è: =e^-1.16=0.313;. Per la prima conseguenza degli assiomi della probabilità, la probabilità che una persona a caso vada dal medico almeno una volta in un anno è =1-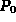=0.687, etc.

• Esempio 2. Calcolare quanti conteggi di decadimenti radioattivi bisogna effettuare per ottenere una precisione del 5%.

  Soluzione. Se si contano N eventi rari, frutto di uno steso processo aleatorio con probabilità costante, l'errore statistico da associare a tale numero è 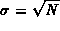in questo modo l'errore relativo o percentuale decresce, all'aumentare di N, come .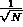
  Quindi per realizzare una misura precisa è necessario aumentare adeguatamente il numero di conteggi da effettuare: in particolare, per ottenere una precisione del 5% occorrerà che sia verificato

  

  Risolvendo questa equazione otteniamo il numero di conteggi necessario per ottenere una precisione del 5%, ossia N=400.

• Esempio 3. Ad un centralino arrivano delle chiamate con una densità media k ogni ora. Supponendo che il numero di chiamate in un qualsiasi intrevallo di tempo sia distribuito secondo la legge di Poisson, calcolare la probabilità con la quale arrivano esattamente 3 chiamate in 2 minuti.

  Soluzione. Il numero medio di chiamate in 2 minuti, dal valore medio sull'intervallo di un'ora, è uguale a:

  

  Applicando la formula della distribuzione di Poisson, otteniamo per m=3 chiamate:

  

La distribuzione di Poisson