Per definire il concetto di covarianza per due variabili aleatorie, dobbiamo prima introdurre la generalizzazione del concetto di momento. Per un sistema di due variabili aleatorie discrete (x,y) si dice momento iniziale di ordine k,s la seguente espressione:
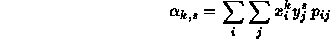
che non è altro che la speranza matematica del prodotto delle potenze k e s delle due variabili e dove pij è la probabilità che il sistema definito dalle due variabili assuma il valore (xi,yj). Analogamente possiamo definire il momento centrale di ordine k,s nel modo seguente:
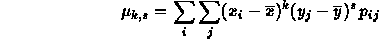
Ovviamente le generalizzazini al caso continuo saranno
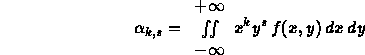
e
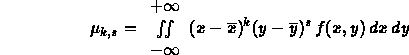
dove f(x,y) è la densità di probabilità del sistema.
Il momento centrale misto del secondo ordine Kx,yha un'importanza particolare:
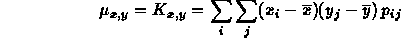
o, nel caso continuo
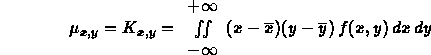
Tale momento è detto covarianza. E` un parametro che, oltre descrivere la dispersione delle variabili, esprime anche la loro relazione. In particolare la covarianza di variabili aleatorie indipendenti è nulla, mentre è diversa da zero se esiste una relazione che lega le variabili considerate. Ma la covarianza caratterizza non solo la dipendenza delle variabili aleatorie, bensì anche la loro dispersione. Infatti nel caso in cui una delle variabili del sistema differisca di poco dal suo valore atteso, la covarianza sarà piccola qualunque sia il grado di legame tra le due variabili.
Dunque per caratterizzare solo il legame tra le variabili si passa dal momento Kx,y ad un'altra grandezza adimensionale detta coefficiente di correlazione.
Caratteristiche
numeriche di sistemi di due variabili aleatorie
Coefficiente
di correlazione
