DISTRIBUZIONI CONTINUE
- Distribuzione ² -

Si dice distribuzione ² con n gradi di libertà la distribuzione della somma dei quadrati di n variabili aleatorie indipendenti, ciascuna delle quali obbedisce ad una legge normale con speranza matematica nulla e varianza pari all'unità.
Considerata cioè la variabile

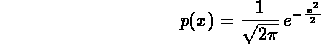
si ha che la nuova variabile ² con definita come

si distribuisce secondo quella che viene chiamata distribuzione ² per n gradi di libertà, ossia

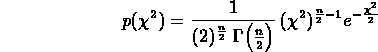
Il numero n delle variabili addende indipendenti rappresenta il numero di gradi di libertà e tale numero costituisce il valor medio della distribuzione in quanto, essendo le singole variabili distribuite secondo una normale standardizzata, i valori medi delle ² sono tutti uguali ad 1.

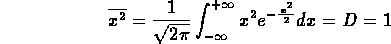
Infatti calcolare il valor medio di ² equivale a calcolare la varianza D di che è appunto uguale ad 1 poichè le variabili sono standardizzate.
La varianza della distribuzione ², invece, è uguale a 2n.

Esempio

Simulazione

Consideriamo una variabile aleatoria X distribuita normalmente: siano le sue realizzazioni in n prove.
Introduciamo la seguente variabile aleatoria

dove 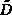è il quadrato della deviazione standard nella sua forma "migliorata" calcolata attraverso le n realizzazioni della variabile X

mentre D è la varianza della distribuzione normale.
Questa nuova variabile obbedisce alla distribuzione ².

Vediamo ora un esempio di test del ². consideriamo un esperimento in cui la distribuzione di Poisson è la distribuzione attesa. Supponiamo di allestire un contatore Geiger per contare le particelle di raggi cosmici che arrivano in una certa regione e inoltre di contare il nimero di particelle che arrivano in 100 intervalli separati di un minuto con i risultati riportati in tabelle

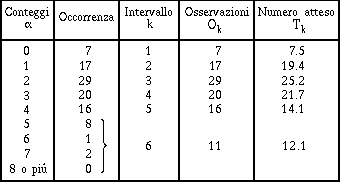
L'osservazione delle occorrenze in tabella suggerisce di raggruppare tutti i conteggi maggiori di 5 in un singolo intervallo.

L'ipotesi che vogliamo verificare è che il numero di conteggi è governato da una distribuzione di Poisson. Poichè il conteggio medio atteso è incognito, dobbiamo prima calcolare la media dei nostri 100 conteggi.

Principali distribuzioni continue