|
Calcolo della
velocitÓ di deriva
|
|
|
Se chiamiamo n il numero delle cariche per unità di volume nel conduttore, la
carica totale, per unità di volume, è data da (q n), con q = -e per gli elettroni.
La velocità delle cariche è
|
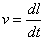
|
|
Il tratto di conduttore percorso nell'intervallo di tempo dt è:
|
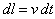
|
|
Attraverso la superficie S nel tempo dt passa una quantità di
carica
|
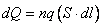
|
|
(S ·dl) rappresenta il volume del cilindro di base S ed
altezza infinitesimale dl occupato dalle cariche che hanno attraversato S.
|
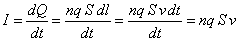
|
|
Dividendo
il primo e l'ultimo membro per S, si ottiene:
|
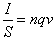
|
|
Quindi la
densitÓ di corrente risulta:
|
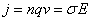
|
|
Segue che la velocità v delle cariche, detta velocità di deriva
o drift, è costante perché
dipende solo da grandezze costanti
|
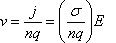
|
![]()