|
Campo elettrico in un conduttore
|
|
|
Un modo
alternativo di descrivere le forze elettriche che si esercitano tra
le cariche è quello di introdurre il
concetto di campo elettrico. Una carica o una distribuzione di
cariche modifica le proprietà
dello spazio circostante in modo tale che esso diventa la sede di forze elettriche:
esprimiamo questo fatto dicendo che lo spazio circostante la carica
è sede di un campo elettrico. Il campo
elettrico E Ŕ definito come la forza che agirebbe su una carica, unitaria
e
positiva, posta in quel punto dello spazio. In generale E varia a seconda della posizione nello spazio.
Consideriamo un conduttore cilindrico di sezione S e lunghezza l, di estremi A e B, percorso dalla corrente I.
|
|

|
|
Detta R la resistenza e
ρ la resistivitÓ
del conduttore, valgono le leggi di Ohm:
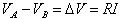
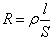
La differenza di potenziale pu˛ essere scritta come:
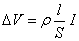
|
|
Supponendo
che il conduttore sia omogeneo possiamo considerare il campo elettrico
E uniforme.
In questo caso il legame tra il campo elettrico e la differenza di
potenziale è:
∆V = E · l
allora:
|
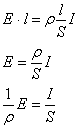
|
|
A questo
punto possiamo introdurre la densità di corrente
j:
|
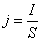
|
|
definita come la corrente che passa attraverso l'unità di area del conduttore, ovvero
come
la carica che attraversa l'unità di superficie nell'unità di
tempo. Dalle due formule precedenti otteniamo:
|
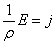
|
|
Possiamo allora scrivere
la resistività come:
|
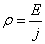
|
|
Talvolta si preferisce usare il reciproco della resistività, detto
conduttività o conducibilità:
|
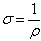
|
|
la densitÓ di corrente in funzione della
conduttivitÓ diventa:
|
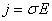
|
|
che riassume le due leggi di Ohm e può essere assunta come
definizione alternativa di conduttori ohmici.
|
|
Calcolo della velocità di deriva (drift velocity)
|
|
Se chiamiamo n il numero delle cariche per unità di volume nel conduttore, la
carica totale, per unità di volume, è data da (q n), con q = -e per gli elettroni.
La velocità delle cariche è
|
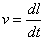
|
|
Il tratto di conduttore percorso nell'intervallo di tempo dt è:
|
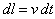
|
|
Attraverso la superficie S nel tempo dt passa una quantità di
carica
|
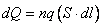
|
|
(S ·dl) rappresenta il volume del cilindro di base S ed
altezza infinitesimale dl occupato dalle cariche che hanno attraversato S.
|
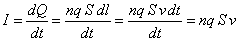
|
|
Dividendo primo e secondo membro per S, si ottiene:
|
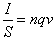
|
|
Quindi
|
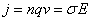
|
|
Segue che la velocità v delle cariche, detta velocità di deriva
o drift, è costante perché
dipende solo da grandezze costanti
|
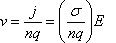
|
![]()