|
Esperimento di Millikan
|
|
|
Con questo esperimento fu dimostrato per la prima volta che la carica
elettrica era quantizzata e ne fu misurato il valore minimo, ossia la carica dell'elettrone.
Millikan sfruttò il moto di piccole goccioline di olio (emulsioni, sospensioni) immesse mediante uno spruzzatore
in una camera, sostanzialmente costituita dalle due armature di un condensatore
caricato ad un potenziale regolabile.
La camera è illuminata per rendere le goccioline osservabili tramite un
microscopio con oculare munito di una scala graduata.
Scelta una gocciolina se ne può misurare la velocità di deriva
(a condensatore scarico) dovuta all'equilibrio fra la forza di
gravità e quella di attrito viscoso con l'aria della camera. La gocciolina possiede delle cariche
elettriche superficiali, indotte dallo sfregamento con il condotto che
la immette nella camera (in alternativa
le goccioline possono essere elettrizzate anche per esposizione a radiazioni ionizzanti).
Applicando una differenza di potenziale alle armature del
condensatore si può allora
esercitare una forza elettrica sulla goccia in modo da fermarla, riportarla in alto, farla ricadere etc.
Ripetendo l’esperienza più volte e con diverse gocce, si osserva che valori del campo elettrico che fermano
le gocce sono tutti multipli di un valore unico, appunto proporzionale alla carica dell'elettrone.
|
|
|
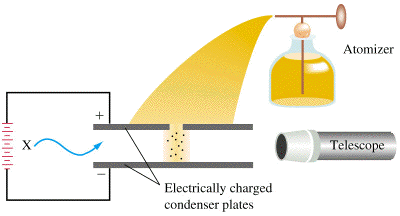
Immagine tratta da http://cwx.prenhall.com/petrucci/medialib/media_portfolio/text_images/FG02_08.JPG
|
|
|
Consideriamo quindi le forze a cui è soggetta la goccia:
- forza peso: F = m g
- forza elettrostatica: F = q ·V/d
- forza di attrito viscoso con l'aria: F = 6ρηvR
con m = massa della goccia, g =
accelerazione di gravità, q = carica sulla goccia, V = potenziale elettrico,
d = distanza tra le armature del condensatore, η = coefficiente di viscosità dell'aria, R = raggio della goccia,
v = velocità della goccia,
ρ = densità della goccia.
|
|
|
La forma della goccia è approssimata a quella di una sfera. A causa della viscosità
dell’aria, il suo moto può
essere considerato laminare essendo R e v sufficiente piccoli.
Se si applica un’opportuna differenza di potenziale V tra le
armature del condensatore, tale che la forza elettrica eguagli la forza peso, la gocciolina resta sospesa in equilibrio. In queste condizioni abbiamo:
|
|
|
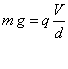
|
|
ovvero
|
|
|
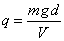
|
|
|
Per ricavare la quantità
di carica q sulla goccia occorre quindi conoscerne la massa.
Per misurare la massa m, si azzera il potenziale e si registra la velocità di caduta
della goccia sotto l'azione della sola forza peso e della forza viscosa; tale velocità è data dalla formula:
|
|
|
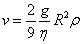
|
|
|
dalla quale, misurando v
(tramite l'uso della scala graduata dell'oculare e di un cronometro), si può
ricavare il raggio R della goccia supposta sferica.
Conoscendo la densità dell'olio e calcolando il volume della
sfera si ricava la massa m
|
|
|
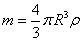
|
|
|
| Infine, si ricava la carica q sostituendo il valore della
massa nella formula |
|
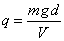
|
|
Poiché le goccioline sono molto piccole, la quantità di carica presente su di esse può essere dell’ordine di una
decina di cariche elementari; misurando allora tale carica in un grande numero di casi si può verificare, nei limiti degli errori
sperimentali, che i valori trovati sono tutti multipli interi di un certo valore che può essere assunto come la carica elementare e.
|
|
|
Il valore della carica elementare ottenuto con l'esperimento di Millikan è
|
|
|
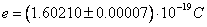
|
|
|
|
![]()