DISTRIBUZIONI CONTINUE
- Distribuzione di Student -

Per ricavare la distribuzione di Student consideriamo una variabile aleatoria y distribuita secondo una distribuzione normale standard, e una variabile x, indipendente da y, avente una distribuzione ² con n gradi di libertà.
Siamo allora interessati a studiare il comportamento della nuova variabile t definita come:

Questa nuova variabile obbedisce alla distribuzione di Student

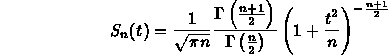
dove la funzione 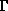è così definita:

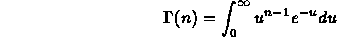
Questa distribuzione presenta due comportamenti differenti a seconda del valore di n: per piccoli valori di n essa approssima la distribuzione di Cauchy, mentre per n grandi approssima la normale.
Generalmente questa distribuzione viene adoperata quando il numero di valori cosiderati è piccolo (n piccolo), quando si studiano eventi molto distanti dal valor medio o quando si verificano entrambe le situazioni.

Infine si noti che gli unici momenti finiti della distribuzione di Student sono quelli di ordine minore di n. In particolare tutti i momenti di ordine dispari sono nulli in virtù della simmetria della distribuzione, mentre tutti quelli di ordine pari superiore ad n sono infiniti.

Esempio

Simulazione

Consideriamo una variabile aleatoria distribuita normalmente: siano le sue realizzazioni in n prove.
Introduciamo la seguente variabile aleatoria

dove 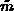è la media calcolata sugli n valori ottenuti

e 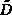è il quadrato della deviazione standard nella sua forma "migliorata"

La nuova variabile t così definita obbedisce alla distribuzione di Student.

Principali distribuzioni continue