NB Non cominciate mai a calcolare prima di aver sviluppato algebricamente la soluzione.
Una corretta tecnica nella soluzione di un esercizio, indipendentemente dalla sua difficoltà, è utile non solo per arrivare al risultato nel tempo più breve, ma anche per comunicarlo ad altri, incluso ad es. il docente, nel modo migliore.
Suggerimenti per la soluzione:
Se necessario disegnate uno o più diagrammi che schematizzano la situazione descritta nel testo del problema, in modo da chiarire la vostra analisi. Spesso ne basta uno. Nei disegni indicate le grandezze fisiche con lettere, mai con numeri.
[Vicino al disegno] sintetizzate in una tabella i dati del problema, rispettando la precisione dei valori (il numero di cifre) e le unità di misura specificate. Controllate di aver riportato correttamente non solo le cifre ma gli ordini di grandezza (esponenti, con il relativo segno);
questa verifica deve essere fatta ad ogni ulteriore passaggio.
[Ri]leggete il testo dell'esercizio attentamente per essere sicuri di aver capito bene che cosa si richiede e in quale forma. Non trascurate le singole parole o addirittura le singole lettere, due enunciati che differiscano anche solo per un monosillabo ('e' al posto di 'o', o viceversa; l'equivalente inglese è un po' più chiaro, 'and' al posto di 'or') danno luogo a risultati del tutto diversi.
Ricavate la formula risolutiva dell'esercizio nella forma esplicita x = f(y,z,t...) dove x è la grandezza richiesta e y,z,t... sono le altre grandezze che intervengono nella soluzione. Questo vi permetterà di identificare eventuali grandezze ridondanti nell'enunciato. Verificate
la correttezza dimensionale della formula risolutiva.
Scegliete il sistema di unità di misura, per es. quello in cui deve essere data la soluzione, ove questo sia richiesto esplicitamente nel testo, oppure quello più comodo per fare i conti. Trasformate i valori delle grandezze che devono essere trasformate, tenendo conto della precisione finale richiesta (tre cifre significative)
e quindi arrotondando nei passaggi intermedi, se proprio non si può evitare di farli, a non meno di quattro cifre. Non trasformate mai più dello stretto necessario, ogni operazione in più è una possibile sorgente di errore e/o di svarione. Evitate il più possibile i passaggi intermedi (cioé impostate tutta la serie di operazioni sulla calcolatrice senza passaggi e riporti): in ciascun arrotondamento è insita una approssimazione, quindi un errore, mentre il portarsi dietro troppe cifre non aiuta, appesantisce il foglio (il calcolo) e fa aumentare il rischio di trascriverne male una, magari proprio fra le prime (a sinistra, fra le più significative) o addirittura un esponente.
Calcolate il valore richiesto, arrotondando il risultato al numrero di cifre significative richieste, tipicamente tre per un numero reale. Ricordate che, a volte, però il risultato è intero ed è importante che lo sia (un sasso, la caselle di una roulette).
Separatamente, per non appesantire la scrittura, controllate le unità.
Calcolate senza la calcolatrice almeno l'ordine di grandezza del risultato che vi aspettate. Ciò permette di verificare di non aver aver fatto proprio errori di calcolatrice (un esponente sbagliato ad es.) o altri
grossolani errori di trascrizione.
Controllate infine che il risultato non violi il buon senso. Ciò può dipendere dai dati (sono scelti a caso), oppure dalla soluzione, ad es. un segno sbagliato o un esponente, un rapporto invertito. Un oggetto che nel vuoto e nel solo campo della gravità cade verso l'alto, una velocità maggiore della costante c di Einstein, una grandezza negativa sotto radice quadrata etc. segnalano la presenza di un errore.
Il buon senso, imparato per l'esame scritto, può essere impiegato utilmente a volte durante l'esame orale, durante il quale può capitare, è bene ricordarlo, un esercizio da svolgere fino al risultato numerico. Gli esercizi all'orale sono semplificati nei numeri e non richiedono l'uso della calcolatrice, che, del resto, non è permessa. All'orale quindi si richiede esplicitamente la capacità di effettuare manualmente le quattro operazioni (somma, sottrazione, moltiplicazione, divisione) nel campo dei numeri razionali e l'estrazione della radice quadrata. È necessario anche ricordarsi le principali
formule della geometria elementare (aree, volumi), nonchè avere una nozione pratica della trigonometria elementare (identità trigonometriche, funzioni trigonetriche di angoli notevoli &tc.).
If you can't solve a problem, you can always look up the answer. But please, try first to solve it by yourself; then you'll learn more and you'll learn faster [Donald E. Knuth, The TEXbook (1983)]
Esempi di risoluzione degli esercizi
Esercizio -1
Un blister per compresse di aspirina è riempito con azoto/N2 alla pressione ambiente di 756.9 mmHg. Si misura la contaminazione di ossigeno/O2 che risulta di 67 ppm [parti per milione] in volume. Qual'è la pressione parziale dell'ossigeno/O2 nel SI? Soluzione
Esercizio 0
Un lingotto formato d'oro e d'argento pesa 4.693 N; immerso nell'acqua esso pesa 4.411 N. Qual è il volume di argento contenuto nel lingotto? (densità oro = 19.3 g/cm3, densità argento = 10.5 g/cm3) Soluzione
Esercizio 1
Un bambino lancia dei sassi contro una parete quadrata di lato 5.44 m in cui sono stati praticati 223 fori quadrati aventi un lato di 9.71 cm. Se il bambino non mira e i sassi sono piccoli rispetto alle dimensioni dei fori, qual è il numero più probabile di sassi che rimbalzerà sulla parete ogni 590 lanci? Soluzione
Esercizio 2
Il coefficiente di diffusione dell'emoglobina in acqua è D = 6.32*10-7 cm2sec-1 a temperatura ambiente 20 gradi C). Calcolare quanta emoglobina diffonderà lungo un tubo orizzontale con sezione di raggio 1.98 cm in 8704.4 ore sotto un gradiente
di concentrazione di 4.472 g/litro per metro. Soluzione
Esercizio 3
Due lamine Polaroid sono poste in contatto fra loro con un angolo di 0.3954 radianti fra le loro direzioni di trasmissione. Se un fascio di luce non polarizzata di ampiezza 137.5 volt/metro passa attraverso il sistema, qual'è l'ampiezza del fascio emergente? Soluzione
Esercizio 4
Un liquido ideale (d.rel = 0.783) scorre stazionario in un condotto orizzontale di sezione variabile. Se la velocità del liquido in corrispondenza della sezione 1 è 0.3952E+03 cm/sec e la sua pressione è 1.3875 atm, quanto vale la pressione del fluido nella sezione 2 dove la velocità è 15.4261 km/h? Soluzione
Esercizio 5
Diverse misure dello sforzo di compressione applicato ad un osso, e della deformazione che ne deriva, forniscono le seguenti coppie di valori:
( 0.894E+07 N·m-2, 0.10 %),
( 0.122E+08 N·m-2, 0.14 %),
( 0.163E+08 N·m-2, 0.18 %). Calcolare il valor medio del modulo di Young dell'osso. Soluzione
Esercizio 6
Un lingotto formato d'oro e d'argento pesa 7.077 N; immerso nell'acqua esso pesa 6.688 N. Qual è il volume di oro contenuto nel lingotto? (densità oro = 19.3 g/cm3, densità argento = 10.5 g/cm3) Soluzione
Esercizio 7
L'acqua che evapora da una piscina può essere schematizzata come se diffondesse attraverso un film di aria spesso 0.1409 cm. Il coefficiente di diffusione del vapor d'acqua in aria a 20 °C è 0.2536 cm2/s. Se l'aria fuori dal film è saturata di vapor d'acqua al 49.34%, qual è la massa d'acqua che evapora al giorno da uno stagno di superficie 0.2087·103 m2? La concentrazione del vapor d'acqua corrispondente alla pressione di vapor saturo è 0.9606 moli/m3 a 20 °C. Soluzione
Esercizio 8
Un corpo pesa 0.3602 N nell'acqua e 0.4189 N nell'olio (densità relativa olio 0.9127). Calcolare la densità, il peso e il volume del corpo. Soluzione
Esercizio 9
Un'auto percorre un'autostrada rettilinea ad una velocità costante di 101.1 Km/h. Una vespa vola dentro l'abitacolo perpendicolarmente alla direzione dell'auto, ad una velocità costante di 0.99 m/s. Se l'abitacolo è largo 157.5 cm, qual è lo spazio percorso dalla vespa durante la traversata di tutto l'abitacolo
rispetto ad un osservatore fermo sul ciglio dell'autostrada? Soluzione
Esercizio 10
La concentrazione massima di piombo permessa in generale in un ambiente senza che si presentino rischi per la salute è 0.1 mg/m3. In un laboratorio di ricerca del volume di 74.92 m3 sono stati trovati 0.000782 ml di piombo (la densità relativa del piombo
è 11.35). Trovare il valore della concentrazione di piombo nel laboratorio e specificare se il valore trovato eccede o meno il limite tollerato. Soluzione
Esercizio 11
Un recipiente sferico di raggio r = 0.9637E+01 cm è riempito di gas perfetto a temperatura T0 = 0.4695E+03 K e a pressione atmosferica. Si riscalda il gas di 0.3697E+02 °C, qual è il modulo della forza esercitata dal gas sull'1.095% della superficie della sfera? Soluzione
Esercizio 12
Una automobile procede su una autostrada ad una velocità di 100 km/h. Qual è lo spazio necessario alla frenata se il coefficiente di attrito degli pneumatici è 0.496 e il ritardo dovuto ai riflessi dell'autista è di 0.179 s? Soluzione
Esercizio 13
Due pesi, uno di 12.33 N e l'altro di 6.70 N, sono appesi alle estremità di un'asta rigida pesante lunga 1.012 m, che ha una densità lineare di massa ρ = 1.911 kg/m. In che punto l'asta va sospesa, affinché rimanga orizzontale? Soluzione1 Soluzione2
Esercizio 14
Un cubetto di ghiaccio di 192.6 g (alla temperatura di 0 °C) viene gettato in un recipiente che contiene 553.9 g di acqua alla temperatura di 51.52 °C. Trovare la temperatura finale del sistema se il ghiaccio fonde interamente. Il calore latente di fusione del ghiaccio è 79.78 cal/g. Si trascurino le perdite. Soluzione
Esercizio 15
Una serie di misure della densità di una sostanza eseguita con diversi metodi dà i seguenti valori: ρ1 = 1.100 g/cm³, ρ2 = 0.1081E+04 kg/m³, ρ3 = 1.035 kg/l, ρ4 = 0.1096E+04 kg/m³, ρ5 = 1.052 g/cm³. Si trovi il valore medio ρ delle misure nel SI. Soluzione
Esercizio 16
Un dolce gelato ha una massa di 726.1 g ed un volume di 1010.7 ml. Se una frazione f = 0.3992 del volume ha una densità relativa pari a 0.7524, qual è la densità assoluta (nel SI) della restante parte del dolce? Soluzione
Esercizio 17
Quanta energia (in joule) bisogna fornire per aumentare di 16.31 K la temperatura di 1.384 l di acqua che si trova inizialmente a temperatura ambiente e a pressione atmosferica? Soluzione
Esercizio 18
Una sfera di piombo di raggio 1.195 cm appesa ad un filo è immersa in un recipiente contenente acqua. Qual è la forza (in newton) che deve esercitare il filo per sostenere la sfera? La densità relativa del piombo è 11.35. Soluzione
Esercizio 19
Un giaguaro può raggiungere la velocità di 96.21 km/h. L'uomo più veloce può raggiungere la velocità di 35 km/h. Se un uomo e un giaguaro sono ad una distanza di 0.6997 km l'uno dall'altro e possono correre entrambi ad una velocità costante pari alla loro velocità massima, quanto tempo impiega il giaguaro a raggiungere l'uomo? Soluzione
Esercizio 20
Quando colpisce la corteccia di un albero la testa di un picchio si ferma dopo essere partita con una velocità iniziale di 0.6942 m/s e aver percorso una distanza di 0.2872 cm. Calcolare la decelerazione in unità dell'accelerazione di gravità g. Soluzione
Esercizio 21
Una bruciatura prodotta dal vapore a 100 °C è più grave di quella prodotta dalla stessa quantità di acqua a 100 °C. Verificare questa affermazione calcolando il rapporto tra il calore che deve essere sottratto a 0.5728E-02 kg di acqua e di vapore per abbassarne la temperatura da 100 °C a 42.05 °C. Si assuma un calore latente di vaporizzazione dell'acqua pari a 2240 J/g e che il calore specifico dell'acqua non vari tra 0 °C e 100 °C. Soluzione
Esercizio 22
Un calamaro di 3.920 kg inizialmente fermo spinge 282.1 g d'acqua alla velocità di 36 km/h in 0.0975 s. Calcolare l'accelerazione del calamaro trascurando la forza di attrito dell'acqua. Soluzione
Esercizio 23
Un tratto di una arteria è ristretto da una placca arteriosclerotica al 18.24% della sua sezione trasversale. Qual è la diminuzione percentuale di pressione in questo punto? La pressione del sangue in una arteria sana è 100 mm Hg e la velocità è 0.120 m/s. La densità del sangue è 1040 kg/m3. Soluzione
Esercizio 24
Si calcoli la corrente continua I che attraversa la batteria nel circuito in figura (V0 = 0.788E+02 V, R1 = 0.5·R2 = 0.25·R3 = 0.890E+03 ohm, L1 = 16.402 mH). 
Soluzione
Esercizio 25
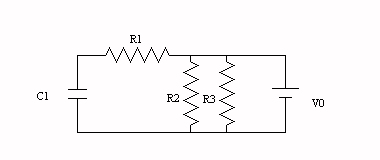
Si calcoli la corrente continua I che attraversa la batteria nel circuito in figura (V0 = 0.871E+02 V, R1 = 0.5·R2 = 0.25·R3 = 0.825E+03 ohm, C1 = 30.497 nF).
Soluzione
Per ulteriori informazioni, chiarimenti o suggerimenti manda un mail
a:
Prof. F. L. Navarria (navarria .at. bo.infn.it)
Copyright © 2016 DFUB
Ultimo aggiornamento 1 Maggio 2016
